11269. Лемурьи вечеринки – базовая

 

В подчинении у короля лемуров Джулиана находится ровно  2 * k лемуров – по два лемура каждого из k видов. Джулиан обожает вечеринки, поэтому каждый вечер устраивает тусовку. Однако в VIP-зоне, к сожалению, хватает мест только для него самого и ещё n лемуров.

Поскольку Джулиан не любит повторяться, он старается каждый раз приглашать в VIP-зону такой набор лемуров, который ранее ещё не встречался. Два лемура одного вида считаются неразличимыми. Два набора лемуров считаются одинаковыми, если они совпадают как мультимножества видов лемуров.

Помогите Джулиану определить, сколько различных вечеринок он сможет провести. Так как ответ может быть очень большим, выведите его по модулю 109 +7.

 

Вход. В одной строке заданы два целых числа  k и n (1 ≤ k ≤ 500 000, 0 ≤ n ≤ 2 * k) – количество видов лемуров и число мест в VIP-зоне (не считая самого Джулиана).

 

Выход. Выведите одно число – количество различных вечеринок по модулю 109 +7.

 

Пример входа 1

Пример выхода 1

3 3

7

 

 

Пример входа 2

Пример выхода 2

4 3

16

 

 

РЕШЕНИЕ

комбинаторика

 

Анализ алгоритма

На n мест некоторые виды будут представлены двумя лемурами, а некоторые одним. Пусть выбрано i пар лемуров (то есть i видов представлены двумя особями). Сделать такой выбор можно  способами. После этого в VIP зоне останется n – 2i свободных мест. Эти места можно занять лемурами из k – i оставшихся видов, выбирая по одному лемуру из каждого. Количество способов выбрать таких лемуров вычисляется по формуле .

Так как значение i может принимать любое целое значение от 0 до k, получаем итоговый ответ как сумму по всем возможным i:

 

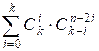
Пример

Рассмотрим второй пример, в котором есть k = 4 пары лемуров и n = 3 места в VIP-зоне. По формуле получаем:

 =  +   = 4 + 12 = 16

Выпишем только ненулевые слагаемые. Значение  будем считать равным нулю, если выполняется одно из трех неравенств: k < 0, n < 0 или k > n.

Обозначим лемуров буквами {a, a, b, b, c, c, d, d}, где одинаковые буквы соответствуют лемурам одного вида.

Слагаемому  = 4 соответствует ситуация, когда ни одна пара лемуров одного вида не выбрана, то есть каждый из трёх выбранных лемуров принадлежит разным видам. Возможные четыре выборки следующие:

 

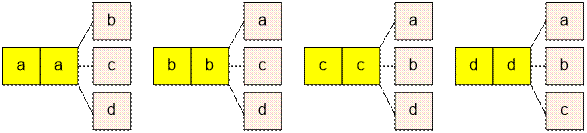
Рассмотрим слагаемое  = 12. В этом случае из одного вида выбираются два лемура (существует 4 варианта такого выбора). На оставшееся одно место выбирается один лемур из трёх оставшихся видов. Таким образом, всего возможно 12 различных вариантов:

 

Очевидно, что разместить на 3 местах по два лемура из двух разных видов невозможно. Поэтому все остальные слагаемые суммы равны нулю.

 

Реализация алгоритма

Объявим константы.

 

#define MAX 1000001

#define MOD 1000000007

 

Объявим массивы:

·        fact содержит факториалы чисел по модулю MOD;

·        factinv содержит значения, обратные факториалам чисел по модулю MOD:

fact[n] = n! mod 1000000007

factinv[n] = n! -1 mod 1000000007

 

typedef long long ll;

ll fact[MAX], factinv[MAX];

 

Функция pow вычисляет степень числа по модулю: xn mod p.

 

ll pow(ll x, ll n, ll p)

{

  if (n == 0) return 1;

  if (n % 2 == 0) return pow((x * x) % p, n / 2, p);

  return (x * pow(x, n - 1, p)) % p;

}

 

Функция inverse находит число, обратное x по простому модулю p. Поскольку p – простое число, по малой теореме Ферма выполняется равенство:

xp-1 mod p = 1 для всякого 1 ≤ x < p

Это равенство можно переписать в виде:

(x * xp-2) mod p = 1,

откуда следует, что обратным к x является число xp-2 mod p.

 

ll inverse(ll x, ll p)

{

  return pow(x, p - 2, p);

}

 

Функция Cnk вычисляет значение биномиального коэффициента по следующей формуле:

 =

 

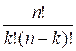
ll Cnk(int n, int k)

{

  return ((fact[n] * factinv[k]) % MOD * factinv[n - k]) % MOD;

}

 

Основная часть программы. Читаем входные данные.

 

scanf("%d %d", &k, &n);

 

Заполняем массивы факториалов fact и factinv.

 

fact[0] = 1;

for (i = 1; i < MAX; i++)

  fact[i] = (fact[i - 1] * i) % MOD;

 

factinv[0] = 1;

for (i = 1; i < MAX; i++)

   factinv[i] = inverse(fact[i], MOD);

 

Вычисляем ответ по формуле 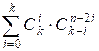.  Значение биномиального коэффициента  считаем равным нулю, если выполняется одно из трех условий: k < 0, n < 0 или k > n.

 

res = 0;

for (i = 0; i <= k; i++)

{

  if (n - 2 * i < 0 || k - i < 0 || n - 2 * i > k - i) continue;

  res = (res + Cnk(k, i) * Cnk(k - i, n - 2 * i)) % MOD;

}

 

Выводим ответ.

 

printf("%lld\n", res);